今回は「ITエンジニアのための機械学習理論入門」の最尤推定による回帰分析のサンプルコードを ruby で実装してみます。書籍のサンプルコードは下記に公開されています。
自然対数
今回は前回までのコードと似ている部分が多く、新しい要素は自然対数のみで、python では自然対数を求めるために numpy.log を使います。
numpy.log
https://docs.scipy.org/doc/numpy/reference/generated/numpy.log.html
ruby では Math.log メソッドを使います。
Math.log
https://docs.ruby-lang.org/ja/latest/method/Math/m/log.html
サンプルスクリプト全体
ruby でのコード全体としては下記のように実装しました。
require 'daru' require 'nyaplot' N = 10 M = [0, 1, 3, 9] def normal_rand(mu = 0, sigma = 1.0) random = Random.new (Math.sqrt(-2 * Math.log(random.rand)) * Math.sin(2 * Math::PI * random.rand) * sigma) + mu end def create_dataset(num) dataset = Daru::DataFrame.new({'x': [], 'y': []}) num.times do |i| x = i.to_f / (num - 1).to_f y = Math.sin(2 * Math::PI * x) + normal_rand(0, 0.3) dataset.add_row(Daru::Vector.new([x, y], index: [:x, :y])) end return dataset end def log_likelihood(dataset, f) dev = 0.0 n = dataset.size.to_f dataset.each_row do |line| x = line.x y = line.y dev += (y - f.call(x))**2 end err = dev * 0.5 beta = n / dev -beta * err + 0.5 * n * Math.log(0.5 * beta / Math::PI) end def resolve(dataset, m) t = dataset.y columns = {} (m+1).times do |i| columns["x**#{i}"] = dataset.x ** i end phi = Daru::DataFrame.new(columns) tmp = (phi.transpose.to_matrix * phi.to_matrix).inv ws = (tmp * phi.transpose.to_matrix) * Vector.elements(t.to_a) f = lambda {|x| y = 0 ws.each_with_index do |w, i| y += w * (x ** i) end y } sigma2 = 0.0 dataset.each_row do |line| sigma2 += (f.call(line.x) - line.y)**2 end sigma2 /= dataset.size return f, ws, Math.sqrt(sigma2) end train_set = create_dataset(N) test_set = create_dataset(N) df_ws = {} fig = Nyaplot::Frame.new M.each_with_index do |m, c| f, ws, sigma = resolve(train_set, m) df_ws["M=#{m}"] = Daru::Vector.new(ws, name: "M=#{m}") plot = Nyaplot::Plot.new sc = plot.add_with_df(train_set.to_nyaplotdf, :scatter, :x, :y) sc.title("train_set") sc.color('blue') linex = (0..1).step(1.0 / (101 - 1)).to_a liney = linex.map do |x| Math.sin(2 * Math::PI * x) end line_answer = plot.add(:line, linex, liney) line_answer.title('answer') line_answer.color('green') liney = linex.map do |x| f.call(x) end line_middle = plot.add(:line, linex, liney) line_middle.title("Sigma=#{sprintf("%.2f", sigma)}") line_middle.color('red') line_upper = plot.add(:line, linex, liney.map {|y| y + sigma }) line_upper.color('red') line_lower = plot.add(:line, linex, liney.map {|y| y - sigma } ) line_lower.color('red') plot.configure do x_label("M=#{m}") y_label('') xrange([-0.05, 1.05]) yrange([-1.5, 1.5]) legend(true) height(300) width(490) end fig.add(plot) end fig.show df = Daru::DataFrame.new({m: [], 'Test set': [], 'Training set': []}) 9.times do |m| f, ws, sigma = resolve(train_set, m) train_mlh = log_likelihood(train_set, f) test_mlh = log_likelihood(test_set, f) df.add_row(Daru::Vector.new([m, test_mlh, train_mlh], index: [:m, 'Test set'.to_sym, 'Training set'.to_sym])) end df.plot(type: [:line, :line], x: [:m, :m], y: ['Test set'.to_sym, 'Training set'.to_sym]) do |plot, diagrams| test_set_diagram = diagrams[0] train_set_diagram = diagrams[1] train_set_diagram.title('Training set') train_set_diagram.color('blue') test_set_diagram.title('Test set') test_set_diagram.color('green') plot.x_label("Log likelihood for N=#{N}") plot.y_label('') plot.legend(true) end
これを jupyter notebook 上で実行すると下記のようなグラフが描画されます。
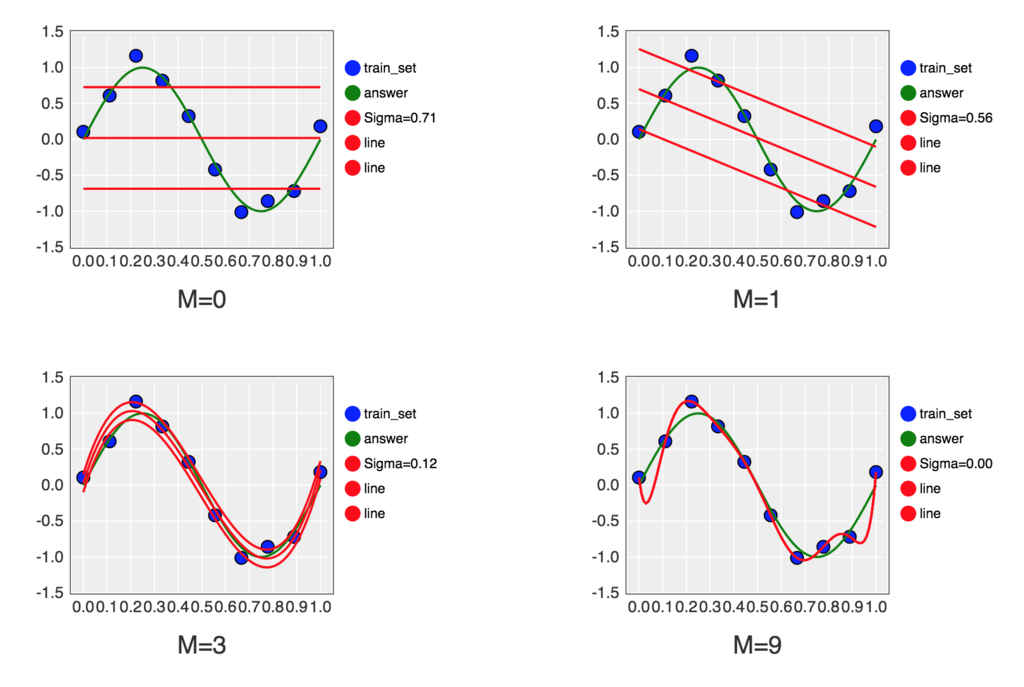
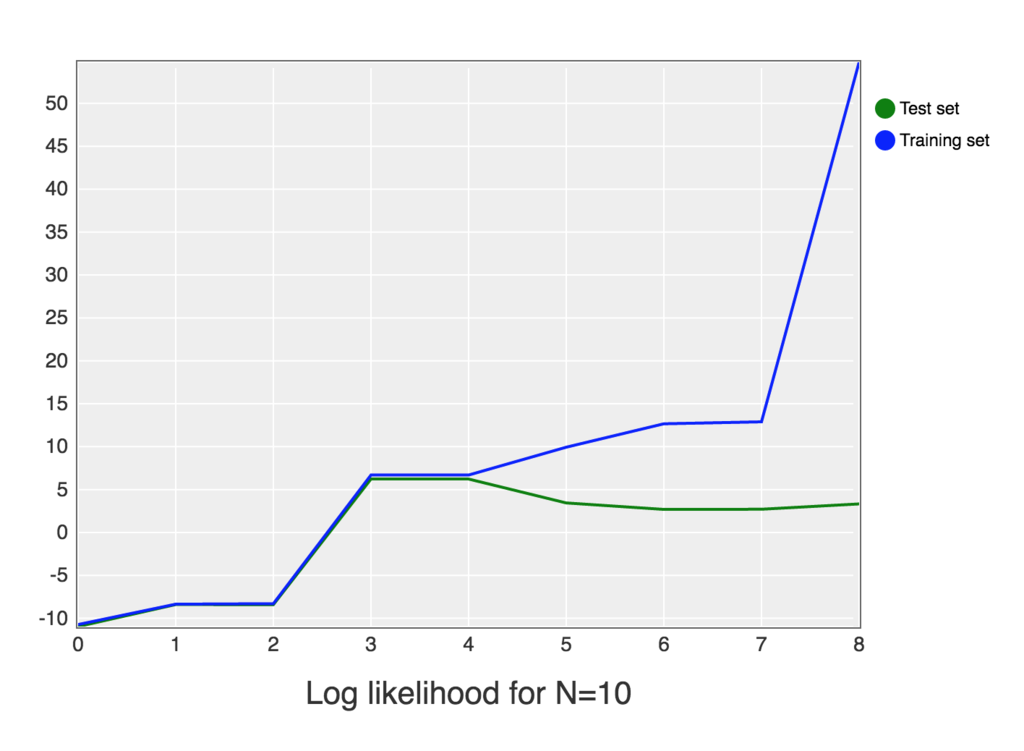
Jupyter Notebook 上での実行結果は下記に公開してあります。
http://nbviewer.jupyter.org/github/h-akanuma/ml4se_study/blob/master/03-maximum_likelihood.ipynb